2020. 3. 5. 07:24ㆍ카테고리 없음
In engineering and science, the solution of linear simultaneous equations is very important. Different analysis such as electronic circuits comprising invariant elements, a network under steady and sinusoidal condition, output of a chemical plant and finding the cost of chemical reactions in such plants require the solution of linear simultaneous equations.In Gauss-Elimination method, these equations are solved by eliminating the unknowns successively. The C program for Gauss elimination method reduces the system to an from which the unknowns are derived by the use of backward substitution method.Pivoting, partial or complete, can be done in Gauss Elimination method. So, this method is somewhat superior to the.
This approach, combined with the back substitution, is quite general. It is popularly used and can be well adopted to write a program for Gauss Elimination Method in C.For this, let us first consider the following three equations:a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3Assuming a1 ≠ 0, x is eliminated from the second equation by subtracting (a2/ a1) times the first equation from the second equation. In the same way, the C code presented here eliminates x from third equation by subtracting (a3/a1) times the first equation from the third equation.Then we get the new equations as:a1x + b1y + c1z = d1b’2y + c’2z = d’2c’’3z = d’’3The elimination procedure is continued until only one unknown remains in the last equation. After its value is determined, the procedure is stopped. Now, Gauss Elimination in C uses back substitution to get the values of x, y and z as:z= d’’3 / c’’3y=(d’2 – c’2z) / b’2x=( d1- c1z- b1y)/ a1 Source Code for Gauss Elimination Method in C.
Gaussian Elimination is an algorithm to solve a system of linear equations of n variables. It uses elementary operations to find the solution to the system of linear equations. It is an efficient method to find the determinant and inverse of a matrix as well. In this program, we will learn how to solve a system of equations using this method. We will also learn how to calculate the determinant of the n x n matrix used in the process. We create a module for 3 matrices a(n,m) for the augmented matrix, b(n) for temporary values of x and x(n) for the final solutions.
We will need this in the main program as well as the subroutine. We read the number of variables, n at the time of execution. We read the augmented matrix from an input file and display it on the screen. Optional: At this stage, we can create another matrix check(n,m) to store the initial values of elements of a(n,m). This can help us substitute the obtained values of x1,x2.,xn later and verify them. We call a subroutine and display the results only in the square matrix a(n,n) is non-singular. This is also called the coefficient matrix.The subroutine needs only the input m or n.
Gaussian Elimination Code
The rest of the values are held in the module. The subroutine generates the arrays and the output sing to tell the status of singularity of the matrix a(n,n). Optional: We can evaluate the L.H.S. And R.H.S by using two simpleone-column arrays of n rows. R.H.S will simply be the initial values ofa(:,m) and L.H.S. Will be a 1.x1+a12.x2+.a1n.xn, a21.x1+a22.x2+.a2n.xn,and so on for all n equations. Are equal for all rows, we have successfully recreated the equation to verify the results.Now for the subroutine:.
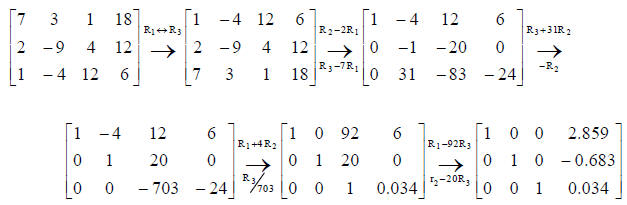
The first step is forward elimination. Starting with the first row,we make sure that the diagonal element has the largest element for itscolumn in that row and all the subsequent rows. If not, we swap rowswith the row from the rows below which has the largest element in thatcolumn. This is an elementary operation. Next, we perform another elementary operation.
We subtract from each subsequent row c=a(k,i)/a(i,i) times the row whose diagonal element large has been set now. So, every a(k,:)=a(k,:)-c.a(i,:). These two steps are repeated for all rows till we get a triangulated matrix. At this stage we can calculate the determinant by multiplying all the diagonal elements a(i,i) together.
If the determinant is non-zero, we proceed with the next step. Else we return to the main program. Finally, we perform back substitution. So, xn=bn/a(n,n). Knowing this, we calculate x(n-1)=b(n-1)-a(n,n).x(n)/a(n-1,n-1).and so on to find values of xn, x(n-1) through x1.We store this result in the array x(n).Let us understand forward eliminate and back substitution further for a 3x3 coefficient matrix.Forward Elimination and TriangularizationRow Swapping Explained furtherBack Substitution to Calculate the Final Values of xn through x1 Backwards. Now for the FORTRAN program,!To use arrays in the programmodule arraysreal, allocatable:: a(:,:), x(:), b(:)end module arrays!To solve a system of equations of n variables using Gauss elimination methodprogram gausepivotuse arraysimplicit noneinteger i,j,n,m,sing,flagreal, allocatable:: LHS(:),RHS(:), check(:,:)!These arrays are optional.
Only to verify resultswrite(.,.) 'Give the size of the coefficient matrix i.e. The number of variables in the system of linear equations'read (.,.) nwrite(.,.) 'The size of the coefficient matrix is ',nopen(unit=1, file='gause.in')m=n+1allocate (a(n,m),x(n),b(n))write(.,.) 'Producing the augmented matrix:'do i=1,nread(unit=1,fmt=.) (a(i,j),j=1,m)write(.,.) (a(i,j),j=1,m)end do!To verify results later. Optionalallocate(check(n,m))!To save the values of the array a(n,m) before they are altereddo i=1,ndo j=1,mcheck(i,j)=a(i,j)end doend docall gauss (m,sing)!To call the subroutine that calculates the resultsif (sing1) thenwrite(.,.) 'the coefficient matrix is singular'else! To display results only if the matrix is non-singularwrite(.,.) 'The given equation has the set of solutions in the order given as follows'write(.,.) (x(i),i=1,n)end ifallocate (LHS(n),RHS(n))!To test the values in array x(n) by substituting them in the linear equation. Optionaldo i=1,nLHS(i)=0do j=1,m-1LHS(i)=x(j).check(i,j)+LHS(i)end dowrite(.,20) 'LHS of row #',i,'=',LHS(i)20 format (a,i3,a,f20.8)RHS(i)=check(i,m)write(.,10) 'RHS of row #',i,'=',RHS(i)10 format (a,i3,a,f20.8)end doflag=0!To set the flag=1 if the L.H.S.